
概要
summary
本書は、建設系学科の学生と技術者のために、この分野でよく使う初等関数の微分と積分(1変数と多変数)を微積分の歩んだ道の歴史に沿って、数学的厳密性は数学書に譲り、道具としての数学の応用をわかり易く整理したものである。構造力学、吊り橋、弾性力学、振動学、測量学、リスク、有限要素法等への応用例と公式を整理している。本書では、運動に関するニュートンの瞬間位置、速度、加速度の考察から微分を説明し、多項式の物理的意味やその微分とテイラー展開、オイラーの公式、部分積分とテイラー展開を柱に整理している。
目次
contents
- まえがき
第1章 運動に対するニュートンの考察と微分法
- 1 補助記事1
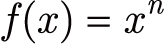 の微分
の微分
第2章 多項式(べき級数)とテイラー展開
- 2.1 多項式
-
- 2.1 補助記事1 ワイエルシュトラス:Weierstrass(独,1815~1897)の定理:コーシイ:Cauchy(フランス,1789~1857)
-
- 2.2 多項式の微分とテイラー展開
-
- 2.2 補助記事1 テイラー(Taylor,英国,1685~1731)、マクローリン(Makulaurin,英国,1698~1746)、ニュートン(Newton,英国,1642~1727)
-
- 2.3 合成関数の微分と2項級数
- (1)合成関数の微分公式
- (2)2項級数
- 2.4 関数
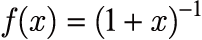 の多項式
の多項式
- (1)マクローリン展開の適用
- (2)ニュートンの方法
- (3)関数
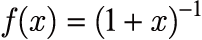 の多項式の適用による各種の多項式の例
の多項式の適用による各種の多項式の例 -
- 2.4 補助記事1 関数の多項式とニュートンの積分と対数
第3章 三角関数、指数関数、対数関数、双曲線関数の微分
- 3.1 三角関数
- (1)角度の定義
- 3.1 補助記事1 円周率
- (2)三角関数の定義
- (3)三角関数の微分と多項式表示
- 3.1 補助記事2 三角関数の和公式と余弦公式
- 3.1 補助記事3 三角関数の多項式
- (1)角度の定義
- 3.2 指数関数と対数関数
- (1)指数関数と対数関数の定義
- 3.2 補助記事1 対数、ネイピア(Napier,スコットランド,1550~1617)
- (2)指数関数と対数関数の微分
- (3)指数関数の多項式表示とオイラーの公式
- 3.2 補助記事2 オイラーの公式と三角関数の公式
- 3.2 補助記事3 オイラーとガウス
- (4)対数関数の多項式表示
- (5)双曲線関数の多項式表示と指数関数、三角関数の関係
- (1)指数関数と対数関数の定義
第4章 微分の応用
- 4.1 微分と曲線の特性値
- (1)P点とQ点の接線の傾き
- (2)P点の曲率半径と曲率
- 4.1 補助記事1 ベルヌーイ・オイラー梁の基礎方程式
- 4.1 補助記事2 オイラーの長柱座屈
- 4.2 微分と最大・最小問題
- (1)体積一定の円柱の最小表面積
- (2)最小の矢板建設コスト
- 4.3 自重による棒の変形解析
- (1)一様断面の棒の変形
- (2)一様断面応力の棒の断面変化
- 4.4 自重によるケーブルのたわみ曲線とカテナリー曲線
- (1)たわみ角が小さい場合のたわみ曲線(放物線)
- (2)厳密なたわみ曲線(カテナリー曲線)
- 4.5 等速円運動と振り子の振動解析
- (1)等速円運動
- (2)振り子の振動解析
- 4.6 2次元弾性力学とモール・クーロンの破壊基準によるランキン土圧
- (1)応力の座標変換と主応力やモールの応力円
- (2)モール・クーロンの破壊基準によるランキン土圧
第5章 多変数関数と微分-偏微分と全微分-
- 5.1 偏微分と全微分
- (1)2変数関数のマクローリン展開とテイラー展開
- 5.2 合成関数の偏微分と全微分
- (1)平面直交座標と極座標の1階偏微分
- (2)平面直交座標と極座標の2階偏微分
- (3)3次元直交座標と円柱座標および球座標のラプラシアン
- 5.3 最大最小問題およびラグランジェの未定係数法
- (1)2変数関数の最大値・最小値
- 5.3 補助記事1 三角測量の角測量の最確値
- (2)ラグランジェの未定係数法
- (1)2変数関数の最大値・最小値
第6章 面積と積分並びに積分と微分の関係
- 6.1 面積
- 6.2 面積と積分および微分との関係
-
- 6.2 補助記事1 微分と積分、ニュートンとライプニッツ
-
- 6.3 積分の重要公式と例題
- (1)部分積分
- (2)テイラー展開と部分積分
- (3)積分による円の面積
第7章 多変数関数の積分
- 7.1 2重積分
- 7.2 変数変換による2重積分
-
- 7.2 補助記事1 行列式による三角形の面積
-
- 7.3 変数変換による積分の有限要素法への応用
- (1)一次元線形要素
- (2)2次元線形三角形要素
- (3)2次元線形四辺形要素
- 7.4 重積分の部分積分によるグリーン定理
- (1)2重積分とグリーンの定理(表現定理)
- (2)ガウスの発散定理
- 7.4 補助記事1 部分積分とガウスの発散定理とグリーンの定理
第8章 土木環境数学で使う公式
- 8.1 微分公式
- 8.2 指数と対数公式
- 8.3 (8,9,10)の公式の導き方
- 8.4 多項式表示
- 8.5 不定積分
- 8.6 定積分
- 8.7 三角関数と双曲線関数
- 参考文献
- 索 引
著者紹介
introduction
助成出版
grant
各種寄付金による出版。
装丁
binding









