土木環境数学Ⅱ

時間と振動数・波数領域による定数係数の微分方程式と波動方程式の解法

著｜原田隆典

著｜本橋英樹

定価2,750円（2,500円＋税）

在庫:あり

仕様：B5判並製

ページ数：173

ISBN：978-4-434-29468-6

発行日：2021/10/20

概要

summary

本書は、建設系学生や技術者のために、例題を使って1階と2階微分方程式、連立1階微分方程式（状態方程式）、波動方程式の時間領域と振動数・波数領域の解法を解説したものである。フーリエ変換は時空間領域と振動数・波数領域を繋ぐので、使い方と高速フーリエ変換を解説した。次に、ラプラス変換とフーリエ変換の関係や留数定理、また、各種微分方程式の数値計算法を整理した。構造物の免震と制震を例に、状態方程式の最適制御の基礎と数値計算例を示した。最後に、地震や外力による地盤振動の3次元と2次元問題の関係を例題とともに解説した。

2.1　時間領域の解法
1. （1）同次方程式の解
  1. 2.1　補助記事1　同次方程式の解の仮定
（2）非同次方程式の特解
（3）非同次方程式の一般解と初期条件を満たす解
1. 2.1　補助記事2　畳み込み積分（Convolution）の模式図による説明
2. 2.1　補助記事3　指数関数のグラフと外力一定の時の解
2.2　振動数領域の解法（フーリエ変換による方法）
1. （1）フーリエ変換とその条件
2. （2）ラプラス変換のアイデアとラプラス変換の概要
  1. 2.2　補助記事1　一般化フーリエ変換とラプラス変換の関係
3. （3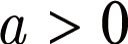）の場合の解法
4. （4）の場合
  1. 2.2　補助記事2　複素積分の留数定理
  2. 2.2　補助記事3　係数の正負で分けて解析しない1階微分方程式の振動数領域の解析
    （ラプラス変換のアイデアを使ったフーリエ変換：一般化フーリエ変換）
5. （5）時間領域と振動数領域の解のまとめ
  1. 2.2　補助記事4　離散フーリエ変換

第3章　2階微分方程式の解

3.1　時間領域の解法
1. （1）同次方程式の解
2. （2）非同次方程式の特解
3. （3）一般解と初期条件を満たす解
3.2　振動数領域の解法
1. （1）の場合
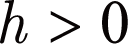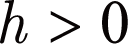2. （2）の場合の振動数領域の解のまとめ
3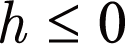. （3）の場合
  1. 3.2　補助記事1　減衰定数零の単振動のフーリエ解析
    （ラプラス変換のアイデアを利用したフーリエ変換：一般化フーリエ変換）
  2. 3.2　補助記事2　単位衝撃力（Unit Impulse）による応答
    （時間領域と振動数領域の1階と2階の微分方程式の解）
3.3　時間領域と振動数領域の単位衝撃力による応答（グリーン関数）と任意外力による応答の関係

第4章　定数係数の連立1階微分方程式（状態方程式）

4.1　概要
1. （1）定数係数の2階微分方程式
2. （2）定数行列係数の2階微分方程式
4.2　同次方程式と非同次方程式の解の概要（時間領域）
4.3　同次方程式の解
1. （1）固有値と固有ベクトル、固有行列と係数行列の対角化
2. （2）係数行列の対角化と対称行列の固有ベクトルの直交性
3. （3）一般解と初期条件を満たす解
4.4　固有値と固有ベクトルに関する性質の整理と例題
4.5　指数関数行列を使う解
1. （1）指数関数行列
  1. 4.5　補助記事1　指数関数行列の例題
2. （2）同次方程式の解
  1. 4.5　補助記事2　指数関数行列と差分方程式の関係
3. （3）非同次方程式の解
  1. 4.5　補助記事3　1自由度振動方程式の指数関数行列（伝達行列）

第5章　係数行列の固有値のみを使う伝達行列の計算

5.1　ケーリー・ハミルトンの定理を使う方法
1. （1）ケーリー・ハミルトンの定理
2. （2）無限級数和の伝達行列の有限級数和表現
3. （3）重根の無い場合の例題
4. （4）重根の有る場合の例題
  1. 5.1　補助記事1　ケーリー・ハミルトンの定理
5.2　シルベスターの恒等式を使う方法
1. （1）シルベスターの恒等式
  1. 5.2　補助記事1　振動方程式の解
5.3　振動数領域の解
1. 1. 5.3　補助記事1　で零でないような場合の解
    （ラプラス変換のアイデアを使う方法:一般化フーリエ変換）

第6章　定数係数の高階微分方程式

6.1　時間領域の解
1. （1）同次方程式の解
2. （2）非同次方程式の特解
6.2　振動数領域の解
1. 1. 6.2　補助記事1　一般化フーリエ変化による2階微分方程式（振動方程式）の解
  2. 6.2　補助記事2　2階微分方程式（片持ち梁のたわみ曲線）
  3. 6.2　補助記事3　4階微分方程式（両端固定梁のたわみ曲線）

第7章　微分方程式の数値計算法

7.1　1階微分方程式の数値解析法（ルンゲ・クッタ法）
7.2　2階微分方程式の数値解析法（ルンゲ・クッタ法）
7.3　2階微分方程式の数値解析法（Nigam・Jennings法）
7.4　2階微分方程式の数値解析法（Newmarkの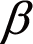法を用いたCloughの増分法）
1. 1. 7.4　補助記事1　（テイラー展開とNewmarkの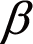法）
  2. 7.4　補助記事2　4次精度のルンゲ・クッタ法とNewmarkの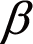法の微分演算子と伝達演算子の関係による整理
  3. 7.4　補助記事3　一定外力を受ける振動方程式の差分法解と理論解
7.5　連立1階微分方程式の数値解析法（直接積分法）
1. 1. 7.5　補助記事1　一定外力を受ける1自由度系の振動
  2. 7.5　補助記事2　一定外力を受ける1質点系の振動の数値計算例

第8章　構造物の免震と制震

8.1　受動的免震・制震の考え方
1. （1）外力を受ける1質点系の免震・制震
2. （2）外力を受ける多質点系の制震
3. （3）受動的制震系の数値計算
  1. 8.1　補助記事1　地震動加速度を受ける1質点系の受動的免震・制震の計算例
8.2　最適制震理論（外力の無い場合の時間に関する連続系の最適制震法）
1. 1. 8.2　補助記事1　スカラーの1階微分方程式の最適制震外力
  2. 8.2　補助記事2　評価関数の最小値とリカッチ方程式（ラグランジェの未定係数法）
8.3　制震理論（外力の有る離散系の最適制震法）
1. 1. 8.3　補助記事1　外力を受ける離散化連立1階微分方程式の最適制震力とリカッチ方程式
  2. 8.3　補助記事2　外力の無い1自由度系の最適制震力と最適応答の数値計算例
  3. 8.3　補助記事3　正定値対称行列Pの計算のための繰り返し法
  4. 8.3　補助記事4　地震動を受ける1自由度振動系の最適応答と制震力
  5. 8.3　補助記事5　評価関数の最小値とリカッチ方程式

第9章　2次元と3次元フーリエ変換による波動方程式の一般解

9.1　2次元波動方程式のSH波（面内問題）
1. （1） SH波の波動方程式
2. （2）振動数・波数領域の解
  1. 9.1　補助記事1　波数・振動数の幾何学的意味とSnellの法則
3. （3）多層の要素剛性行列
4. （4）水平多層弾性体の全体の剛性方程式
5. （5）水平1層弾性体の地震波応答
9.2　2次元波動方程式のP・SV波（面外問題）
1. （1） P・SV波の波動方程式
2. （2）振動数・波数領域の解
3. （3）多層の要素剛性行列
4. （4）水平多層弾性体の全体の剛性方程式
9.3　2次元と3次元波動方程式の関係（振動数・波数領域）
1. （1） 3次元波動方程式
2. （2）振動数・波数領域の解
3. （3）調和平面波の特性と座標変換
4. （4） 3次元波動方程式の解と2元波動方程式の解の関係

参考文献
索　引

著者紹介

introduction

原田隆典（はらだたかのり）

宮崎大学名誉教授。山口県生まれ。1975年九州工業大学開発土木工学科卒業。1980年東京大学大学院工学研究科博士課程修了（土木工学専攻、工学博士）、宮崎大学助教授（工学部土木工学科）。1997年宮崎大学教授（工学部土木工学科）。2018年宮崎大学名誉教授。同年、宮崎大学発ベンチャー企業（株）地震工学研究開発センター技術顧問、現在に至る。

本橋英樹（もとはしひでき、中国名：王宏沢〈おうこうたく〉）

（株）IABC地震・津波研究室取締役室長。中国遼寧省生まれ。2001年宮崎大学工学部土木環境工学科卒業。2006年宮崎大学大学院工学研究科博士後期課程修了（システム工学専攻、博士（工学））、（株）耐震解析研究所。2009年帰化。2011年宮崎大学発ベンチャー企業（株）地震工学研究開発センター主任研究員。2017年現在に至る。

※発行時の奥付より